Building Reliable Distributed Systems with Formal Modelling

Building Reliable Distributed Systems with Formal Modelling

Authors:

Designing distributed systems has always demanded more than writing correct code. The real difficulty lies in what happens between the lines - the unpredictable world of networks where messages can be delayed, reordered, or even duplicated. In payment infrastructures, a rare sequence of retries might accidentally double-credit a user, or a message lost in transit could leave balances inconsistent. These failures don’t emerge in simple test runs; they appear when concurrency introduces countless possible event orderings.

Traditional testing covers a handful of scenarios, but the unseen combinations often carry the highest risk. These hidden interactions are what make distributed systems both fascinating and fragile. What is needed is an approach that exposes those invisible corners, enabling teams to reason about correctness with mathematical precision before the first line of production code exists.

The Promise of Formal Modelling

One way to confront the fragility of distributed systems is through formal Modelling -the practice of creating a mathematical description of a system that makes its behaviour explicit and analysable before implementation. Instead of code, the design is expressed in three parts:

• State variables that capture the system’s condition at any point in time (such as account balances or message queues).
• Actions or transitions that define how the system moves from one state to another (for example, sending or processing a payment).
• Invariants that must always hold true (like ensuring total money remains conserved).

With this structure, a distributed system can be studied as a state machine. Formal Modelling tools systematically explore every possible state transition, not just a small sample of scenarios chosen for testing. Model checkers such as TLC for TLA+ examine the space of possible executions, flagging any sequence that violates an invariant.

• When violations occur, they provide a concrete trace showing exactly how the system drifts into an invalid state.
• When no violations appear within the explored bounds, the design earns strong assurance that it behaves as intended under concurrency.

The real benefit of formal Modelling lies in shifting error detection from late-stage testing to early-stage design, exposing flaws long before production. For domains like digital payments or decentralised ledgers, that assurance can mean the difference between resilience and costly failure.

TLA+ and TLC in a Nutshell

Among the many approaches to formal Modelling, TLA+ has become a widely adopted choice for reasoning about distributed systems. Created by Leslie Lamport (the inventor of Paxos and LaTeX), TLA+ (Temporal Logic of Actions) is not a programming language but a specification language. Instead of describing how a system executes, it focuses on what the system is allowed to do in precise mathematical terms. This shift in focus means that rather than writing procedures, one specifies possible behaviours and verifies whether they meet critical properties.

TLA specifications are evaluated using TLC, its model checker. TLC provides a systematic way to examine system behaviour:

• It explores every possible interleaving of actions within the bounds defined by the model.
• It checks if any sequence of events leads to an invariant being broken.
• If all invariants hold, the design gains strong assurance of correctness.
• If a violation occurs, TLC generates a counterexample trace, a step-by-step path showing how the system drifts into an invalid state.

This combination provides two complementary advantages. TLA+ gives a clear way to describe distributed protocols, while TLC supplies the computational power to uncover flaws that human reasoning or limited testing might miss. Together, they transform correctness from an abstract goal into something that can be checked with mathematical discipline.

Modelling a Simple Credit Transfer

To demonstrate how formal Modelling uncovers hidden flaws, consider a payment scenario with two users, Alice and Bob. It reflects the core of many financial systems, where balances are maintained and credits move asynchronously between parties.

Scenario:

• Alice and Bob each start with 2 credits.
• Alice can send 1 or 2 credits to Bob by enqueuing a message (representing a payment request).
• Bob processes incoming messages one at a time, adding the specified amount to his balance.

The key invariant to preserve is:

Alice_balance + Bob_balance + Credits_in_flight = 4

(i.e. the total money in the system should always be 4.)

This ensures that no matter how transfers occur, the total credits in the system remain conserved.

A TLA+ specification of this system can be expressed with only a few variables, including Alice’s balance, Bob’s balance, the message queue, and a counter for message IDs. The following snippet defines the state and actions:

Step 1: Defining the First Model

                    --------------------------- MODULE AccountTransfer ---------------------------
EXTENDS Naturals, Sequences

VARIABLES alice, bob, msgs, nextId
vars == <<alice, bob, msgs, nextId>>

(* Recursive sum of message amounts *)
RECURSIVE SumAmts(_)
SumAmts(s) == IF Len(s) = 0 THEN 0 ELSE s[1].amt + SumAmts(Tail(s))

Init ==
  /\ alice = 2
  /\ bob   = 2
  /\ msgs  = << >>     \* empty message queue
  /\ nextId = 1

SendCredit(a) ==
  /\ a \in {1,2}
  /\ alice' = alice - a
  /\ msgs'  = Append(msgs, [id |-> nextId, amt |-> a])
  /\ nextId' = nextId + 1
  /\ UNCHANGED bob

ProcessMsg ==
  /\ Len(msgs) > 0
  /\ LET m == Head(msgs) IN
       /\ bob' = bob + m.amt
       /\ msgs' = msgs  \* (message remains until we implement discard)
  /\ UNCHANGED <<alice, nextId>>

Next ==
  \/ \E a \in 1..alice : SendCredit(a)
  \/ ProcessMsg

Spec == Init /\ [][Next]_vars

(* Invariant: total money (in accounts + in messages) stays 4 *)
MoneyConserved == alice + bob + SumAmts(msgs) = 4

                

At first glance, this model appears correct. Each send reduces Alice’s balance, each process increases Bob’s balance, and the invariant seems satisfied. But when checked with TLC, the model immediately breaks.

Step 2: Finding the Bug with Model Checker

When the initial model is verified using TLC against the Money Conserved invariant, the checker immediately reports a violation. The counterexample reveals how the system drifts into an invalid state due to duplicate processing of the same message.

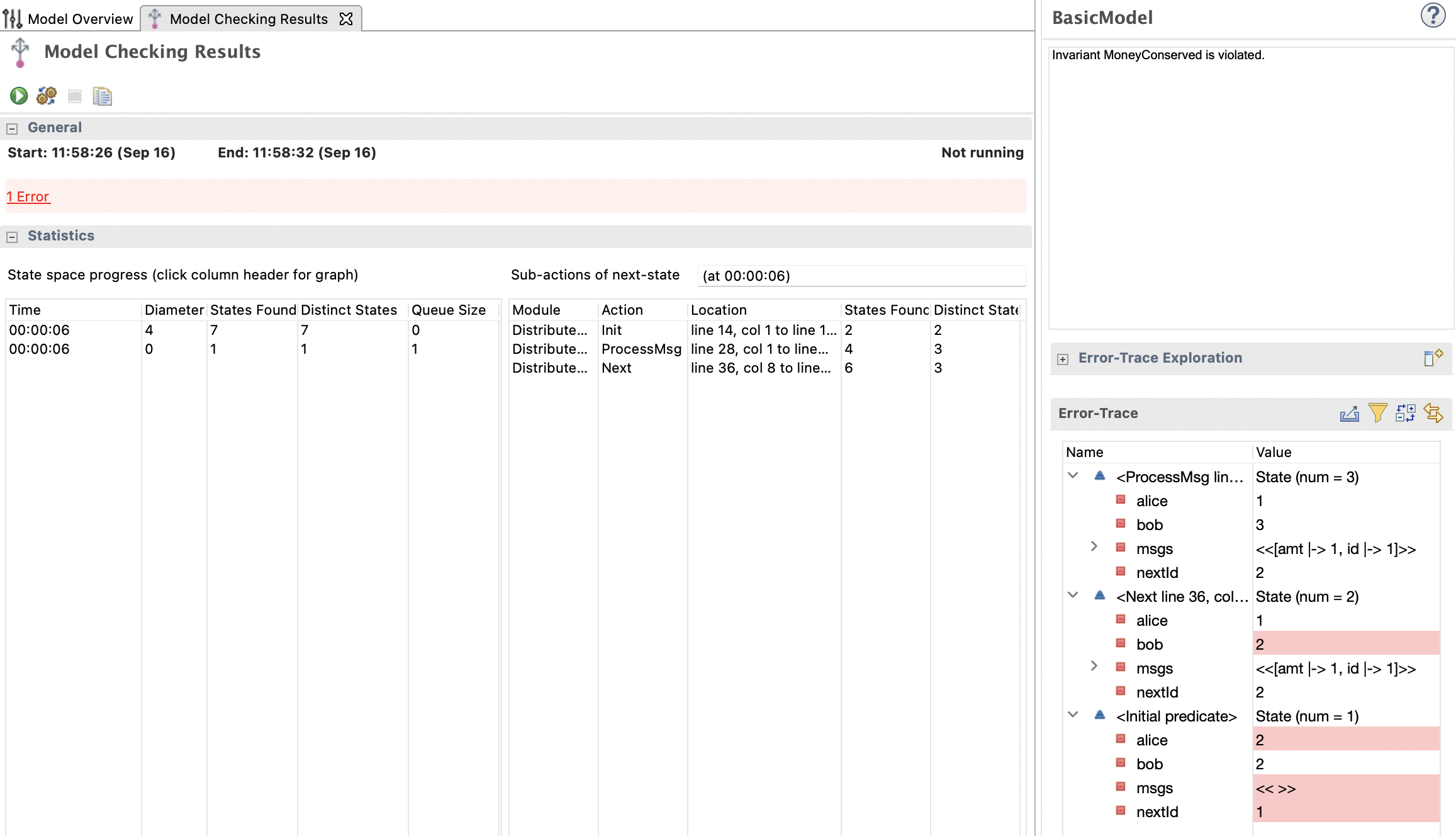
Execution:

I. Alice enqueues two credits of amt=1 each (id=1, id=2).
State: Alice = 0, Bob = 2, messages in flight = 2.

II. Bob processes a message, but it is not removed from the queue.
State: Alice = 0, Bob = 3, messages in flight = 2.

Final state:

Alice = 0

Bob = 3

Credits_in_flight = 2

Total = 5, which breaks the invariant Alice + Bob + Credits_in_flight = 4

This outcome demonstrates how retries or duplicates, which are common in unreliable networks, can cause the system to over-credit Bob without reducing Alice’s balance further.

What looked correct on paper has been proven unsafe under concurrency, thanks to exhaustive model checking.

Step 3: Refining the Model to Fix the Bug

The trace highlights the core problem. Nothing in the model prevents Bob from applying the same message more than once, so retries or duplicates lead to inflated balances and the invariant fails.

To fix this, the model needs a way to remember which transfers have already been applied.

• A processed set is introduced that stores the IDs of completed messages.
• Each time Bob picks up a message, he checks whether the ID is already in the set.
• If the ID exists, the message is ignored. If it does not, the balance update is applied and the ID is added to the set, ensuring no transfer can be counted twice.

                    VARIABLES alice, bob, msgs, processed, nextId
vars == <<alice, bob, msgs, processed, nextId>>

Init ==
  /\ alice = 2
  /\ bob = 2
  /\ msgs = << >>
  /\ processed = {}       \* set of IDs already applied
  /\ nextId = 1

ProcessMsg ==
  /\ Len(msgs) > 0
  /\ LET m == Head(msgs) IN
       /\ IF m.id \in processed
          THEN /\ msgs' = Tail(msgs)
               /\ UNCHANGED <<alice, bob, processed, nextId>>
          ELSE /\ bob' = bob + m.amt
               /\ processed' = processed \cup {m.id}
               /\ msgs' = Tail(msgs)
               /\ UNCHANGED <<alice, nextId>> 
                

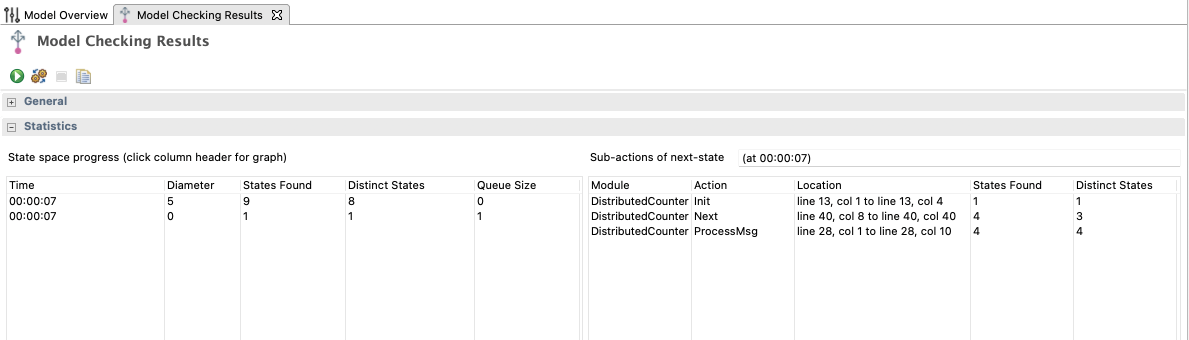
Step 4: Validating the Fix

With the refined specification in place, the behaviour of the system changes noticeably.

• If Bob encounters a message whose ID is already present in the processed set, he simply removes it from the queue without touching the balances.
• If the ID is new, the transfer is applied, and the ID is added to the set, ensuring the same message cannot be counted twice.

When this corrected model is checked again with TLC, the MoneyConserved invariant holds across every explored execution path within the given bounds. The earlier flaw of Bob’s balance growing incorrectly due to duplicates is eliminated, and the system behaves consistently with its intended guarantees.

In practical terms, the model checker has demonstrated that under the modelled assumptions, the invariant cannot be broken.

Lessons Learned and Practical Implications

This walkthrough highlights lessons that resonate strongly with the design of real-world payment infrastructure.

• Concurrency bugs are subtle: Even a minimal credit-transfer model exposed a serious flaw. Real distributed systems like ledgers or routers face far more intricate interleavings, making such issues harder to catch without formal reasoning.
• Models expose what tests miss: Testing checks a handful of cases, while a model checker systematically explores all possible paths. In the example, only the model checker revealed the duplicate-processing bug before implementation.
• Small models are powerful: Under fifty lines of TLA+ uncovered a real-world bug pattern. Creating small models for critical components can save weeks of downstream debugging.
• Shift-left error detection matters: Catching flaws during design reviews is far cheaper than fixing them in production. Large-scale systems already use this approach, and financial infrastructure benefits even more given its sensitivity to correctness.

These lessons go beyond the above scenario. NPCI’s various payment products collectively handle billions of transactions per month. Subtle errors such as duplicate transfers, out-of-order settlements, or inconsistent ledger updates could have severe consequences. Formal Modelling provides a way to validate the soundness of reconciliation, settlement, and consensus protocols before deployment, ensuring that correctness is proven rather than assumed.